Problem solving rates ratios and proportions

Ratios & Proportional Relationships

Then, students encounter the concept of aspect ratio, which is simply the ratio of a rectangle's width to its height, and solve a variety of problems involving aspect ratio. Next, students learn how rates can be used to convert measurement units.

This method is in addition to the methods for converting measurement units that are explained in Math Mammoth books on decimals. It does not mean that students should "change over" and forget what they have learned earlier — it is simply a different method for doing the conversions.

Some students may choose one method over another; some may be able to master all of the methods. Most will probably choose one method they prefer for doing these conversions.

After this, we turn our attention to proportions which is an equation of two ratios. The lessons show how to solve proportions using cross-multiplying and how to set up proportions the correct way. We also study briefly what cross-multiplying is based on it is not a magic trick!

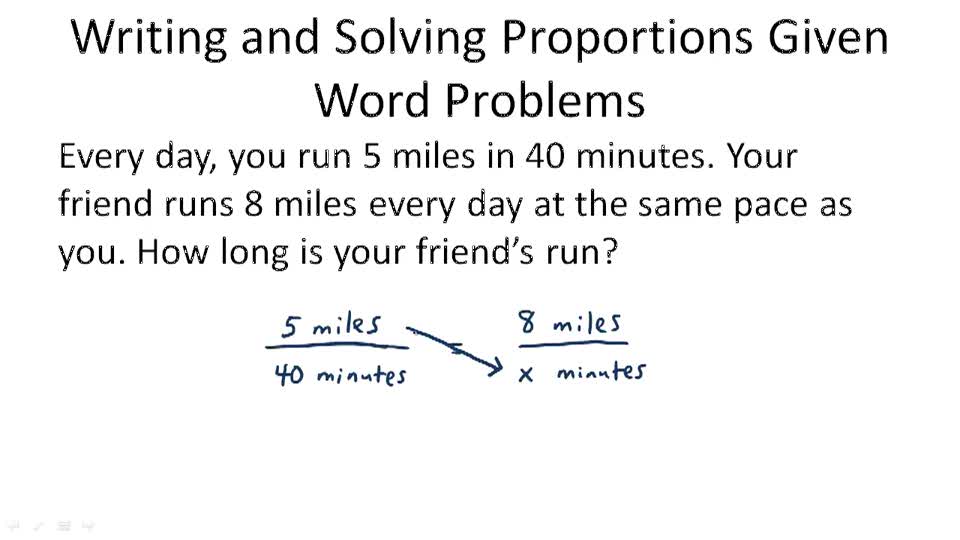
The concept of direct variation is introduced in the lesson Proportional Relationships. There are 16 ducks and 9 geese in a certain park.

Ratio and Proportions Worksheet With Answer Key

Express the ratio of ducks to geese in all three formats. Consider the above park. Express the ratio of geese to ducks in all three formats. The numbers were the same in each of the above exercises, but the order in which they were listed differed, varying according to the order in which the elements of the ratio were expressed.

Grade 7 » Ratios & Proportional Relationships

In ratios, order is very important. Let's return to the 15 men and 20 women in our original group. This points out something important about ratios: The ratio "15 to 20" refers to the absolute numbers of men and women, respectively, in the group of thirty-five people.

How many of the birds are geese? Generally, ratio problems will just be a matter of stating ratios or simplifying them. Express the ratio in simplest form: This reduced fraction is the ratio's expression in simplest fractional form. When both values in a ratio have the same unit, there should generally be no unit on the reduced form.

In contrast to the answer to the previous exercise, this exercise's answer did need to have units on it, since the units on the two parts of the ratio, the "miles" and the "gallons", do not "cancel" with each other.

Proportions

Conversion factors are simplified ratios, so they might be covered around the same time that you're studying ratios and proportions. For instance, suppose you are asked how many feet long an American football field is.

You know that its length is yards. First, I'll need to convert the "two feet four inches" into a feet-only measurement. Since four inches is four-twelfths, or one-third, of a foot, then: Since this is a "real world" word problem, I should probably round or decimalize my exact fractional solution to get a practical "real world" sort of number.

I will set infant temperament essay my ratios with the assessed valuation on top, and I will use "v" to stand for the value that I need to find. One piece of pipe 21 meters long is to be cut into two pieces, with the lengths of the pieces being in a 2: What are the lengths of the pieces?